Le Guide pour bien débuter sa LAS : Ici
 Calendrier de l'Avent du Tutorat
Calendrier de l'Avent du Tutorat
















Le Guide pour bien débuter la LAS : Ici
Tutoriel Forum : Ici
Planning des Séances Tutorat et EB : ICI
Errata : Séances Tutorat et EB, Annatuts, Ronéos
Centres de Téléchargement : ICI !
Réponses des Profs : ICI !
Annales : Achat, Corrections Officieuses
Annatuts : 2024-2025, Sommaire
Tut'Oriente : ICI
Guide de Réorientation : ICI
TUT' RENTRÉE S2 - INFOS ET INSCRIPTIONS : Ici
TUT' RENTRÉE S2 : Programme - Planning Vidéos
Newsletter n°13 : ICI
 Calendrier de l'Avent du Tutorat
Calendrier de l'Avent du Tutorat
















Le Guide pour bien débuter la LAS : Ici
Tutoriel Forum : Ici
Planning des Séances Tutorat et EB : ICI
Errata : Séances Tutorat et EB, Annatuts, Ronéos
Centres de Téléchargement : ICI !
Réponses des Profs : ICI !
Annales : Achat, Corrections Officieuses
Annatuts : 2024-2025, Sommaire
Tut'Oriente : ICI
Guide de Réorientation : ICI
TUT' RENTRÉE S2 - INFOS ET INSCRIPTIONS : Ici
TUT' RENTRÉE S2 : Programme - Planning Vidéos
Newsletter n°13 : ICI
![[Résolu] [Résolu]](././styles/prosilver/imageset/icon_topic_solved.gif) Question Physique
Question Physique
Règles du forum
Utilisez la fonction recherche (en haut à droite) avant d'ouvrir un nouveau sujet.
Soyez respectueux, et pour faciliter le travail des tuteurs, ne posez qu'une question par sujet puis passez-le en résolu après avoir reçu votre réponse.
Utilisez la fonction recherche (en haut à droite) avant d'ouvrir un nouveau sujet.
Soyez respectueux, et pour faciliter le travail des tuteurs, ne posez qu'une question par sujet puis passez-le en résolu après avoir reçu votre réponse.
3 messages
• Page 1 sur 1
![[Résolu] [Résolu]](././styles/prosilver/imageset/icon_topic_solved.gif) Question Physique
Question Physique
Hello, j'aimerai bien que quelqu'un m'explique la question B, j'ai du mal à comprendre.
Merci beaucoup !
-

ShepardME - Carabin confirmé
- Messages: 71
- Inscription: 17 Aoû 2017, 16:27
- Localisation: Passerelle du Normandy SR-2
- Année d'étude: PCEM2
- Prénom: SAMUEL
Re: Question Physique
Bonjour ! 
Alors, tout d'abord, cet item est relativement complexe, c'est tout-à-fait normal s'il te pose problème !
 Ensuite, ce qui t'intéresse c'est comment on en arrive là ?
Ensuite, ce qui t'intéresse c'est comment on en arrive là ?
Commençons par le commencement, i.e. par les définitions !
Le prof donne une propriété importante de la force de Coulomb (je le précise rapidement, ici on va utiliser la force de Coulomb pour trouver une énergie potentielle associée à nos charges puisque la force électrique est par définition la force de Coulomb) : "pour une distribution de charges donnée, la force de Coulomb est additive".
Traduisons rapidement cette phrase ; cette propriété nous dit en fait, que lorsque l'on se trouve avec plusieurs charges (réparties de n'importe quelle manière), on pourra modéliser les différentes forces de Coulomb (ici je parle de forces au pluriel puisque la force de Coulomb s'exercera à différentes reprises, à chaque fois entre 2 charges) comme s'il n'existait en vérité qu'une seule force.
Revenons à notre QCM. Ici, tu as 4 charges différentes et distinctes, 2 charges positives et 2 négatives.
Tu auras ainsi plusieurs couples de charges :
 2 couples de charges opposées séparées d'une distance a :
2 couples de charges opposées séparées d'une distance a :
Puisque les charges sont opposées, comme tu peux le voir sur le schéma, la force de Coulomb sera attractive et sera donc ENTRE tes 2 charges.
 1 couple de charges opposées, séparées d'une distance 3a :
1 couple de charges opposées, séparées d'une distance 3a :
Même raisonnement que pour les 2 couples précédents, charges opposées donc force attractive
 2 couples de charges identiques, séparées d'une distance 4a :
2 couples de charges identiques, séparées d'une distance 4a :
Ici, les charges sont identiques, la force de Coulomb est donc répulsive et comme tu peux le voir sur les schémas, elle "s'éloigne" de nos charges
 1 couple de charges opposées, séparées d'une distance 5a :
1 couple de charges opposées, séparées d'une distance 5a :
Encore une fois, nos charges sont opposées donc notre force de Coulomb est attractive et se trouve entre nos 2 charges
Maintenant que nous avons repéré nos différents couples, nous pourrons définir la valeur de la force de Coulomb pour chacun de nos couples de charges et à partir de là, nous aurons l'énergie potentielle associée (car la force est la dérivée de l'énergie potentielle). De manière générale, la formule de l'énergie potentielle associée à la force de Coulomb s'écrit : . On a donc :
. On a donc :
 Pour les 2 couples de charges opposées séparées d'une distance a :
Pour les 2 couples de charges opposées séparées d'une distance a :

 Pour le couple de charges opposées séparées d'une distance 3a :
Pour le couple de charges opposées séparées d'une distance 3a :

 Pour les 2 couples de charges identiques séparées d'une distance 4a :
Pour les 2 couples de charges identiques séparées d'une distance 4a :

 Pour le couple de charges opposées séparées d'une distance 5a :
Pour le couple de charges opposées séparées d'une distance 5a :

Ensuite, il faut se souvenir de la propriété énoncée plus haut ; "pour une distribution de charges donnée, la force de Coulomb est additive". Ainsi, on va considérer les différentes forces comme une seule, en les additionnant. Cette "unique" force finale aura une énergie potentielle associée, on pourra donc obtenir une unique force potentielle associée à l'ensemble de nos charges, qui sera alors égale à la somme de toutes nos énergies potentielles, on a alors :

NB : j'ai directement multiplié par 2 les énergies potentielles lorsque 2 couples ont la même énergie potentielle
Ensuite, on factorise simplement notre calcul pour simplifier notre immense fraction, ce qui nous donne :
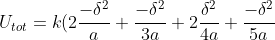=k\frac{\delta ^{2}}{a}(-2-\frac{1}{3}+\frac{2}{4}-\frac{1}{5}))
Enfin, en calculant, on a donc :
On retrouve bien la réponse de l'item B !
Désolée d'avoir pris autant de temps pour te répondre, je voulais vraiment faire une réponse construite et détaillée
En espérant que cela réponde à tes interrogations !
Bon courage pour la suite


Alors, tout d'abord, cet item est relativement complexe, c'est tout-à-fait normal s'il te pose problème !

Commençons par le commencement, i.e. par les définitions !

Le prof donne une propriété importante de la force de Coulomb (je le précise rapidement, ici on va utiliser la force de Coulomb pour trouver une énergie potentielle associée à nos charges puisque la force électrique est par définition la force de Coulomb) : "pour une distribution de charges donnée, la force de Coulomb est additive".
Traduisons rapidement cette phrase ; cette propriété nous dit en fait, que lorsque l'on se trouve avec plusieurs charges (réparties de n'importe quelle manière), on pourra modéliser les différentes forces de Coulomb (ici je parle de forces au pluriel puisque la force de Coulomb s'exercera à différentes reprises, à chaque fois entre 2 charges) comme s'il n'existait en vérité qu'une seule force.
Revenons à notre QCM. Ici, tu as 4 charges différentes et distinctes, 2 charges positives et 2 négatives.
Tu auras ainsi plusieurs couples de charges :
Puisque les charges sont opposées, comme tu peux le voir sur le schéma, la force de Coulomb sera attractive et sera donc ENTRE tes 2 charges.
Même raisonnement que pour les 2 couples précédents, charges opposées donc force attractive
Ici, les charges sont identiques, la force de Coulomb est donc répulsive et comme tu peux le voir sur les schémas, elle "s'éloigne" de nos charges
Encore une fois, nos charges sont opposées donc notre force de Coulomb est attractive et se trouve entre nos 2 charges
Maintenant que nous avons repéré nos différents couples, nous pourrons définir la valeur de la force de Coulomb pour chacun de nos couples de charges et à partir de là, nous aurons l'énergie potentielle associée (car la force est la dérivée de l'énergie potentielle). De manière générale, la formule de l'énergie potentielle associée à la force de Coulomb s'écrit :
Ensuite, il faut se souvenir de la propriété énoncée plus haut ; "pour une distribution de charges donnée, la force de Coulomb est additive". Ainsi, on va considérer les différentes forces comme une seule, en les additionnant. Cette "unique" force finale aura une énergie potentielle associée, on pourra donc obtenir une unique force potentielle associée à l'ensemble de nos charges, qui sera alors égale à la somme de toutes nos énergies potentielles, on a alors :
NB : j'ai directement multiplié par 2 les énergies potentielles lorsque 2 couples ont la même énergie potentielle
Ensuite, on factorise simplement notre calcul pour simplifier notre immense fraction, ce qui nous donne :
Enfin, en calculant, on a donc :
On retrouve bien la réponse de l'item B !
Désolée d'avoir pris autant de temps pour te répondre, je voulais vraiment faire une réponse construite et détaillée

En espérant que cela réponde à tes interrogations !

Bon courage pour la suite


-
Amandab - Carabin Geek
- Messages: 511
- Inscription: 10 Fév 2018, 21:46
- Année d'étude: DCEM2
- Prénom: Amandine
Re: Question Physique
Merci infiniment pour la réponse
-

ShepardME - Carabin confirmé
- Messages: 71
- Inscription: 17 Aoû 2017, 16:27
- Localisation: Passerelle du Normandy SR-2
- Année d'étude: PCEM2
- Prénom: SAMUEL
3 messages
• Page 1 sur 1
Retourner vers QCM divers (DM, annatut's, annales...)
Qui est en ligne
Utilisateurs parcourant ce forum: Aucun utilisateur enregistré et 0 invités


