Alors en fait il fallait vous servir des données de l'énoncé, on passe d'un milieu avec un indice n = 1 (l'air) à n' =1,5 = 3/2 et on cherche des interférences destructives.
De cela vous saviez que les formules des différences de marches étaient :

\lambda)

Soit :
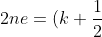\lambda)
Par simplification on obtenait :
\lambda}{2n})
Ici, je ne demandais pas uniquement de calculer l'épaisseur minimale qui correspond au cas où k=0 (J'ai fait la démonstration dans la ronéo il me semble).
Pour k = 0 vous obteniez l'épaisseur minimale pour avoir des interférences destructives :

Seulement, je vous demandais la ou LES épaisseurs possibles, il fallait donc calculer en utilisant les différents k (qui appartient aux entiers naturels rappelons le).

Là, il y avait deux solutions : refaire le calcul à chaque fois, soit utiliser ma méthode un peu plus rapide (uniquement valable pour le cas ci présent, pour les autres cas, la proportionnalité sera différente).
En fait, dès que vous augmentez votre k d'une unité (donc que vous le passez de 0 à 1 par exemple), vous le convertissez à 2/2 et l'ajoutez au 1/2 de la parenthèse.
Admettons que vous passiez de 0 à 1, votre k passe de 0 à 2/2 et votre parenthèses de 1/2 à 3/2.
Si vous simplifiez, vous obtiendrez


Ceci est valable pour tous les entiers pour notre cas :
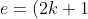e_{min})
C'est juste une autre manière d'écrire votre équation en gros!

Si k = 1 : Déjà fait en dessus!

Si k = 2 :
e_{min}= 5 e_{min} = 500 nm)

Si k = 3 :
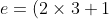e_{min}= 7 e_{min} = 700 nm)
Vous voyez que vous avez atteint les valeurs maximales de l'énoncé à 700 nm! Ainsi, les valeurs possibles étaient 100, 300, 500, 700 et ainsi de suite...
Vu que dans le QCM vous aviez que 100, 300 et 700 : c'était donc les bonnes valeurs!
C'est compris pour tout le monde?


 TUTRICE D'ODONTOLOGIE 2020/2021
TUTRICE D'ODONTOLOGIE 2020/2021 


 Tuteur de Physique 2018 - 2019
Tuteur de Physique 2018 - 2019 
 Tuteur de Physique 2018 - 2019
Tuteur de Physique 2018 - 2019 

 Tuteur de Physique 2018 - 2019
Tuteur de Physique 2018 - 2019 
 Tuteur de Physique 2018 - 2019
Tuteur de Physique 2018 - 2019 
 Tuteur de Physique 2018 - 2019
Tuteur de Physique 2018 - 2019 