Hello !
Alors, allons-y par étape
Item A :
On utilise le PFD parce que la vitesse dépend de la force gravitationnelle. On aurait pu utiliser uniquement la formule de l'accélération si nous avions étudié la Lune indépendamment de la Terre. Ici comme la vitesse de la Lune dépend de l'attraction exercée par la Terre, il faut en tenir compte dans le calcul.
Item B :
Ici, on fait des mathématiques déjà un peu plus avancées :
)
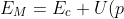Le système qu'on étudie, c'est la Lune, donc ça nous donne :
\times v(Lune)^{2}}{2})
En revanche, il est vrai que l'énergie potentielle associée à la force gravitationnelle n'est pas donnée dans le cours.
Il fallait donc la retrouver :
Il faut donc se baser sur la propriété du cours qui est que la force est la dérivée de l'énergie potentielle. Donc l'énergie potentielle est la primitive de la force.
Il faut donc maintenant retrouver en fonction de quoi on va dériver. La constante de gravitation est, comme le dit son nom, une constante, donc on s'en fiche. Ensuite, la masse de la Terre et la masse de la Lune sont données dans l'énoncé, donc on les considère comme fixes. Au final, il nous reste simplement la distance Terre-Lune, qui n'est pas évoquée dans l'énoncé. C'est également la seule variable restante, et il apparaît logique d'intégrer en fonction d'une distance.
Donc on primitive en fonction de la distance Terre-Lune :
=-\frac{G_{T}\times m_{Terre}\times m_{Lune}}{d_{TL}})
Edit : Cette démonstration n'est pas la bonne, il faut aller voir ma réponse suivante pour avoir la bonne méthodo pour ce genre de QCM 
Enfin, on additionne l'énergie cinétique et l'énergie potentielle retrouvées pour obtenir l'énergie mécanique :
\times v(Lune)^{2}}{2}-\frac{G_{T}\times m_{Terre}\times m_{Lune}}{d_{TL}})
Item C :
Ici, il fallait juste simplifier l'égalité obtenue dans l'item précédent (dis-moi si tu veux que je détaille ça aussi
)
Item D :
On utilise la formule du moment cinétique, à savoir
La Lune étant une masse ponctuelle gravitant autour de la Terre, on va utiliser la formule correspondante, ce qui nous donne :
si on simplifie par le rayon.
Maintenant, on a déterminé l'expression du carré de la vitesse à l'item A, donc on peut remplacer la vitesse ici :
Cependant, on a la distance Terre Lune qui apparaît à la fois au numérateur en dehors de la racine, et à la fois au dénominateur dans la racine. Donc on multiplie à l'intérieur de la racine le numérateur et le dénominateur par la distance Terre Lune :
Du coup au dénominateur on a
donc on peut le sortir de la racine. Du coup on simplifie à l'extérieur de la racine par
et on se retrouve avec :
Du coup, si on multiplie la masse par 3, ça multiplie le moment cinétique par 3, et si on divise la distance Terre-Lune par 81, ça divise le moment cinétique par 9 (bonjour la racine), donc au final, le moment cinétique est divisé par 3.
Je crois que là je pouvais difficilement plus détailler ce QCM
En tout cas, bravo à toi si tu es arrivé jusqu'ici dès la première lecture, parce que franchement, il fallait s'accrocher ! Du coup j'espère que c'est bon pour toi et que tu as mieux compris ce QCM. Il est très dans l'esprit Sepulchre, donc il est +++ à travailler et comprendre, et il te donne une idée du genre de QCM que le prof fait tomber.
Bon courage à toi, et accroche-toi !
Calendrier de l'Avent du Tutorat
![[Résolu]](././styles/prosilver/imageset/icon_topic_solved.gif "[Résolu]"){kind=icon}
merci de m'expliquer 
