Coucou !
 Dans cet exercice :
Dans cet exercice : 
on tire au sort
43 fraises parmi 50 ;

on s'intéresse à la proba qu'
aucune des 3 fraises défectueuses ne se retrouve dans les 43 tirées au sort.
On se retrouve avec : 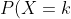=\frac{C_{3}^{0}C_{50-3}^{43-0}}{C_{50}^{43}})
.
C'est une solution, en plus c'est un calcul au final faisable, sachant que 0! = 1.
Mais ce n'est
pas la seule solution possible  Tout simplement, imagine qu'à la place de tirer 43 fraises au sort pour les 43 étudiants, tu tires au sort les 7 que tu n'attribueras pas à des étudiants. Tu veux alors que les 3 fraises défectueuses se retrouvent dans les 7 que tu tires au sort.
Tout simplement, imagine qu'à la place de tirer 43 fraises au sort pour les 43 étudiants, tu tires au sort les 7 que tu n'attribueras pas à des étudiants. Tu veux alors que les 3 fraises défectueuses se retrouvent dans les 7 que tu tires au sort.  N = 50
N = 50, toujours ;
 D = 3
D = 3 toujours aussi ;
 n = 7
n = 7 ;
 k = 3
k = 3.
C'est mieux ?

En tout cas ne t'inquiète pas, si tu avais trouvé n = 43 et k = 0, tu as compris le principe de la loi hypergéométrique ! Je voulais juste vous apprendre à
regarder un problème différemment (voire trouver un calcul plus facile à faire), mais ça a peu de chances de tomber au concours !!
VP Com
Carabins Ex Machina
BDE Médecine 2019-2020
Tutrice de Biostats 2018-2019
Ronéiste d'Anatomie 2018-2020
"Statisticians, like artists, have the bad habit of falling in love with their models" - G.B.

 ???
???


